Post-Malthusian AI

And other ways around a superhuman bind

In previous essays I have argued that human wages can stay high and rising even with superhuman AIs in the economy, but there is an extremely simple model of superhuman AI that locks human wages down, possibly well below subsistence levels:

1. Say a superhuman AI is one that’s more productive than humans at all tasks in the economy. That means the marginal product of a unit of AI labor is greater than the marginal product of human labor for all tasks.

2. In any reasonably competitive market, this means that AI wages must be higher than human wages.

3. AI wages are simultaneously bounded by a Malthusian constraint where they must fall to the cost of copying another unit of AI labor. If wages were higher than this, investors would just copy more until costs rose and wages fell.

These three facts together mean that human wages must be lower than the cost to copy a unit of superhuman AI labor. This upper bound on human wages could be below subsistence levels.

Rising AI Costs

The easiest way out of this bind is to deny that AIs will become superhuman. If humans retain an advantage or exclusivity in some tasks, we can take solace in the previous examples of partial automation that raised human wages, we can expect the human bottleneck on a 99% automated economy to be extremely valuable due to Baumol’s cost disease, and we can expect the gains from technological progress to accrue to labor as the scarce factor in production.

The chance of everlasting human superiority is significant, but it is not large enough to ignore the possibility of superhuman machines. If human superiority does come to an end, there are other ways we might avoid rock-bottom wages.

A straightforward idea is that the cost of spinning up an extra unit of AI labor, that upper bound on human wages, might rise and thus allow human wages to rise with it. After all, LLM scaling laws guarantee that compute requirements for each decrement in training loss rise faster-than-polynomially. New chain-of-thought paradigms further raise the compute cost of running these models. GPT-o3 cost thousands of dollars per task to score 88% on the Arc eval.

Not all increases in the cost of AI labor look good for human outcomes though. If the cost of AI is driven mainly by something that humans also need, like energy, then it’s not clear we would come out ahead. Noah Smith makes this point in his post on human comparative advantage with AIs.

Post-Malthusian AI

Another way out of low human wages is breaking the Malthusian constraint that keeps the superhuman upper bound low.

The first two assumptions of the simple model above seem unassailable to me. We’re defining superhuman AI to be better than humans at everything and how could a resource that’s better at everything earn a return lower than its inferior competition?

But that third assumption, the Malthusian constraint, is the dangerous one. There are lots of people in the world that are better than me at all tasks, so their wages will always be higher than mine. Still, I can find plenty of gainful employment because even though those people earn wages far above the cost of human replication and subsistence, they aren’t feverishly copying themselves.

Not so with AIs. Humans don’t get to claim the difference between the costs of subsistence and the prevailing wage for their children (to the chagrin of Robin Hanson), but the owners of AI do capture that residual. So anytime some technological advance or demand shock raises the returns to AI labor, these owners are paid to expand the supply of AI labor as fast as possible until any gaps between returns and costs are closed.

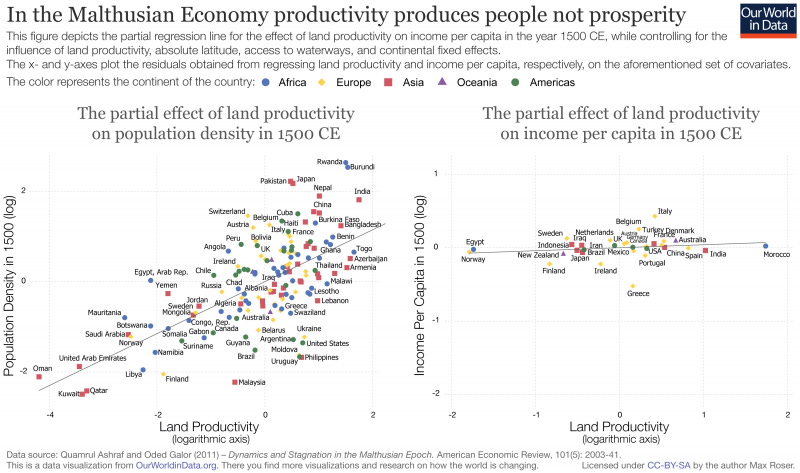
But one thing to notice about this Malthusian constraint on AI wages is that it used to apply to humans too. When a human civilization was on productive land, or had a string of good harvests, or even invented a technology that raised output, per capita incomes did not rise, population did. Every productivity gain just led to more mouths to feed.

Eventually, humans escaped this Malthusian cycle. It wasn’t because of the demographic transition, that came later after per capita incomes had been rising for a few centuries. Instead, the Malthusian constraint was broken because technological progress started raising wages faster than population growth could lower them.

In the 1993 paper Population Growth and Technological Change: One Million B.C. to 1990, economist Michael Kremer models exactly this transition.

Kremer starts with an extremely simple model. Income is produced with people, land, and technology. Land is fixed and the population always expands to bring per capita income to subsistence levels, so population growth is determined by technology. Simultaneously, technological progress is endogenous to the population. Ideas come from people: more people ==> more ideas ==> faster population growth ==> faster ideas and so on. This implies that population grows faster as it gets larger; hyperbolic growth. This leads to an infinite growth singularity but surprisingly fits the data well.

In the simple model, the Malthusian constraint is strictly enforced. Population growth rates adjust instantly after changes in technology so that the economy is never out of equilibrium and per capita incomes are always constant at subsistence level.

When technological progress is slow, and population growth is sensitive to income changes, the simple Malthusian model is an accurate approximation. Wages and population growth rates can stay close to subsistence for long periods as technology inches along. If there are negative shocks, like plagues or wars, those can reset any gains.

Eventually, the feedback loop between population and technological progress takes hold and there is a period of accelerating growth. But to keep this going, population growth soon needs to rise above physical and biological limits. So it levels off while technological progress hums along and raises per capita incomes, thus breaking the Malthusian constraint.

How does this connect to AI? Well, economists often make similar assumptions to Kremer’s simple model of Malthusian population growth for capital stocks. Capital stocks always grow to close the gap between returns and costs, so AI wages stay at subsistence levels. This is bad news when human wages are locked down below those levels.

This assumption of equilibrium in the capital markets is usually reasonable because expanding capital stocks don’t also raise the rate of technological progress. But when we’re talking about superhuman AIs that can do everything humans can but better, then that stock of “capital” clearly will raise technological growth rates and cause permanent disequilibrium in the return on capital for the same reasons that broke humanity out if its Malthusian cycle.

So human wages may face this upper bound from superhuman AIs, but that upper bound will be rising rapidly as technological progress accelerates beyond that pace at which the AI labor force can expand.

A similar result is found in Scenarios for the Transition to AGI by Anton Korinek & Donghyun Suh which is generally pessimistic about the prospect for human wages under the broad automation guaranteed by superhuman AIs. But when they consider that technological progress itself might be automated in section 4.2 they find that

Even if automation induces wages to collapse to the returns to capital, rapid technological progress form the automation of R&D allows workers to benefit from he advancement of AI. More generally, the force described in this subsection is plausible, and sufficient progress in AI will likely lead to rapid technological advances and increases in living standards.

Collusion and Demographic Transition

There are other, non-exclusive ways that AI wages might remain in permanent disequilibrium above the cost of copying them.

The first of these is a pure analogy to the human experience: an AI demographic transition. This seems unlikely because none of the forces pushing humans to have less kids: quality-quantity tradeoffs, opportunity costs, and cultural change, apply to AIs since they don’t have to invest any time in creating copies.

A second possibility is some kind of stable collusion between AI owners or the AIs themselves to prevent too much copying and thus preserve higher wages. Something like an AI union that monopolizes the supply of AI labor and restricts quantity to keep the price high.

I am still optimistic about humanity’s economic future overall, perhaps mostly because of substantial probability mass on a world where AI systems never become fully superhuman. If AIs do become superhuman, then it becomes much harder to imagine legitimate economic value for humans, but it’s not impossible. Automated technological progress in a rapid feedback loop can always outpace Malthusian constraints and keep human wages high even as they are locked down below the wages of superhuman AIs.